Copyright © 2007-2018 Russ Dewey
Correlation and Prediction
The evidence produced by observational research is called correlational data. Correlations are patterns in the data.
The technical term for a coincidence is a correlation. "Co-relation" means essentially the same thing as "co-incidence" or things occurring together.
What is a correlation?
Correlations, observed patterns in the data, are the only type of data produced by observational research. Correlations make it possible to use the value of one variable to predict the value of another.
For example, one could use Daniel Stern's finding from the previous page, that mothers and newborns with a good relationship tend to synchronize their movements. From this one might predict that babies how are "out of sync" with their mothers might fuss and cry significantly more than other babies.
Why is correlational data so useful?
If a correlation is a strong one, predictive power can be great. Consider this figure, from data produced by a 1992 study at the University of Illinois. Researchers asked 56,000 students about their drinking habits and grades, to see how drinking might correlate with performance in school.
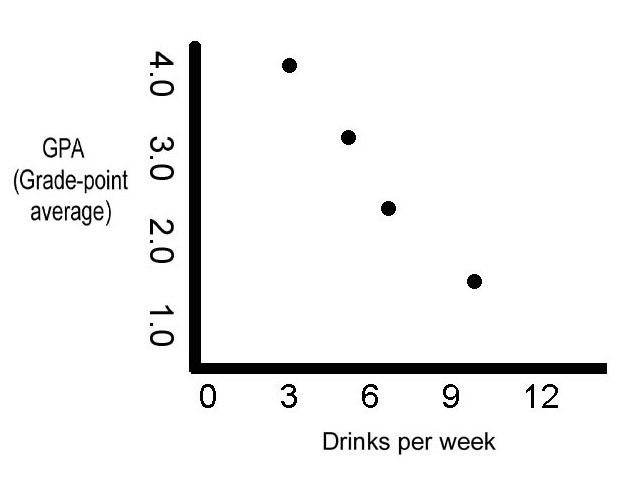
A negative correlation
The results are clear. The more a student drank, the worse was that student's grade-point average. B students (those with a 3.0 GPA) averaged 5 drinks per week, while D students (with a 1.0 GPA) averaged 10 drinks per week.
Using the correlation shown in this graph, you could predict that a person who drank a six pack of beer every day would be likely to flunk out of school.
This is a negative correlation, which means that one variable goes up as the other goes down. As the amount of alcohol consumed goes up on the graph, the corresponding GPA goes down. A positive correlation is one in which variables go up or down together, producing an uphill slope.
What is a positive or negative correlation?
To be more accurate, we should change the label on the X-axis of the graph to "Self-report of drinks consumed per week." This was undoubtedly self-report data (nobody was observing the drinking habits of 56,000 people).
This is a good time to apply some critical thinking skills to an operational definition. We do not know if self-
Perhaps people who get good grades are more likely to lie about drinking. The data do not rule out this explanation. All we know from this study is what people said about how much they drank.
Why should the label on the X axis be changed?
Any type of correlation can be used to make a prediction. However, a correlation does not tell us about the underlying cause of a relationship.
All we know from the Illinois data is that drinking was negatively correlated with grade-point average. The possible explanations are many.
Perhaps (1) alcohol makes people stupid, or (2) higher-achieving students are more likely to lie and say they do not drink even if they do, or (3) the students who tend to drink tend to be poorer students to begin with, or (4) people who are hung-over from a drinking binge tend to skip class, or (5) students in academic trouble drink in order to drown their sorrows after receiving bad grades.
There could be dozens of possible explanations for the correlation. The number of possible cause-effect explanations for any correlation is limited only by your imagination and ingenuity in thinking up possible explanations for an observed relationship.
For purposes of making a prediction, the underlying reason for a correlation does not matter. As long as the correlation is stable–lasting into the future–one can use it to make predictions. What a correlation does not tell you is why two things tend to go together.
Do you need an accurate cause-effect analysis to make predictions?
A study at Virginia Tech found a negative correlation between drinking and grades similar to the one from the Illinois study. It was a somewhat smaller correlation. The Virginia Tech group also gathered self-report data indicating that students who engaged in drinking binges were sometimes too hung over the next day to attend class.
Their data supported this with a correlation between drinking and absenteeism. In this way, the Virginia Tech study began to investigate possible factors underlying the correlation between drinking and low grades.
It is also possible that different factors are important at different schools, or in different countries. In France, drinking might not correlate with bad grades at all. A typical report of a correlation is based on one group of people, at one time, in one place. It does not necessarily reveal a universal truth.
This is another reason replication is important. When an important finding is replicated at different places and times, or with different groups of people, we find out how robust or dependable is the correlation. We may also get hints about the factors that underlie a correlation.
How can replication help to clarify factors underlying a correlation?
Correlations can be useful even if we have no theory to explain them. That does not matter if all we want to do is make predictions. All we need is a reliable correlation. We may not even care if self-reports of drinking are accurate or valid, as long as people are consistent in their self-reports.
Which is more important for making a prediction, validity or reliability?
If the observed relationship between self-reported drinking and grades lasts into the future (if it is reliable) then we can make a prediction based on people's self-reports. "People who say they drink X amount will end up with a grade-point average of about Y."
Write to Dr. Dewey at psywww@gmail.com.
Don't see what you need? Psych Web has over 1,000 pages, so it may be elsewhere on the site. Do a site-specific Google search using the box below.
